High orbit, low orbit - a satellite altitude game
25 Dec 2016This is a model I wrote some time ago, a very stylized special case of a more general recursive model I’m currently working on. Hopefully, the more general model will feature as a chapter of my dissertation, and this might be a subsection of that chapter. I think it’s a sort of interesting model in its own right, even apart from the setting.
The basic motivation is the “orbital debris” problem: as satellites are launched into orbit, there are some debris that accumulate and pose a threat to other objects in the orbital environment. There’s a pretty big literature on this in the aerospace engineering and astrophysics communities, and the popular press has written about this as well. I’ve blogged about a couple papers on the subject before (physics/engineering, economics).
The basic intuition is pretty straightforward and well-known in economics: pollution is a negative externality, firms don’t face the full cost of polluting the environment, they overproduce pollution relative to the socially optimum level. I’m not going to present the planner’s solution, but in the stylized model here firms can cooperate to reduce the amount of debris produced. Without cooperation, they’ll end up choosing higher orbits and producing more debris. The debris can destroy satellites (and that is bad).
In this model I’m focusing on how a firm’s optimal choice of altitude in low-Earth orbit is affected by another firm’s altitude choice. This is an inter-firm externality, which is a little different from the usual consumer-facing externality, but is conceptually similar to strategic substitutability in oligopoly games.
The model setting
Consider an environment with two orbits, high (H) and low (L). We can think of these as spherical altitude shells, similar to the approach described in Rossi et. al (1998).
There are 2 identical firms, each with 1 satellite per period. Debris decays completely after 1 period. Collisions completely destroy a satellite, and generate no debris. Satellites last 1 period, and then are properly disposed of. This lets me talk about dynamics while keeping the decision static.
\(O_i \in \{H,L\}\) is the orbit chosen by firm \(i\) for its satellite. The probability that firm \(i\)’s satellite survives the period is \(S_i(O_i, O_j)\). \(Y_i(O_i, O_j)\) is the probability of a collision between two satellites in the same orbit*. Putting a satellite in orbit \(H\) generates some debris in orbit \(L\) for that period. \(D_L\) is the probability a satellite in the low orbit is destroyed by debris from a satellite in the high orbit**.
*We could say that satellites never collide with each other, but the analysis carries through as long as satellites generate some collision probability for other satellites in the same shell. I think this is generally true, since objects like final stage boosters, random bits that break off, or dead satellites which are not properly disposed of generate such probabilities.
**The idea here is that debris orbits decay toward Earth. This is more relevant for objects in low-Earth orbit, which is what I’m thinking about with this model.
The returns from owning a satellite are normalized to 1, so that we can focus on the probabilities \(S_i\). With the above definitions, we can define the satellite survival probabilities for firm \(i\) as
\[\begin{align} S_i(H,H) ~&= 1 - Y_i(H,H) & \equiv \gamma_{HH} < 1 \cr S_i(L,L) ~&= 1 - Y_i(L,L) & \equiv \gamma_{LL} < 1 \cr S_i(H,L) ~&= 1 & \equiv \gamma_{HL} \cr S_i(L,H) ~&= 1 - D_L(L,H) & \equiv \gamma_{LH} < 1 \end{align}\]So being the only satellite in the high orbit is the best position to be in, since you’re not at risk from debris or the other satellite. It seems reasonable to assume that \(\gamma_{HH} = \gamma_{LL}\) as long as the altitude shells aren’t too large.
The really important assumption is the relationship between \(\gamma_{LH}\) and \(\gamma_{HH}\). If \(\gamma_{HH} > \gamma_{LH}\) (case 1, debris is more likely to cause a collision than a satellite), we’ll end up with one Nash equilibrium in pure strategies. If \(\gamma_{HH} \leq \gamma_{LH}\) (case 2), we can have up to three Nash equilibria in pure strategies. When we relax the assumption that debris decays completely at the end of the period and allow debris growth, we’ll have transitions between the two cases.
Solving the model
Case 1: \(\gamma_{HH} > \gamma_{LH}\)
The game matrix:
| H | L | |
|---|---|---|
| H | \(\underline{\gamma_{HH}}, \underline{\gamma_{HH}}\) | \(\underline{1}, \gamma_{LH}\) |
| L | \(\gamma_{LH}, \underline{1}\) | \(\gamma_{LL}, \gamma_{LL}\) |
(Best responses are underlined. Row player is the first entry, column player is the second.)
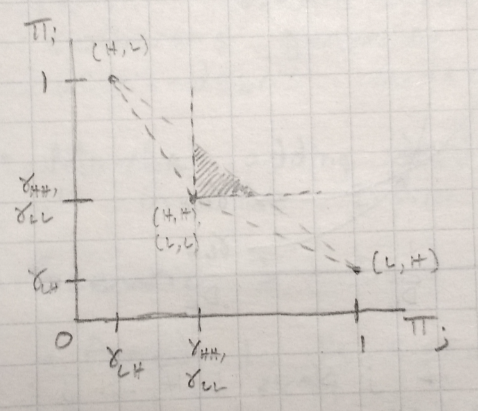
The only Nash equilibrium in pure strategies here is for both firms to go high, \((H,H)\). I call this case “orbital pooling”.
The folk region:
(The images in this post are all photos of diagrams I drew in pencil in my notebook many months ago.)
This case is like a prisoner’s dilemma. Neither firm wants to be in the low orbit when the other firm can go high and make them take on risk. Both firms want to try to be the only firm in the high orbit with no risk - you can see this in the folk region diagram and best responses. So, both firms end up high and with risk.
Case 2: \(\gamma_{HH} \leq \gamma_{LH}\)
The game matrix:
| H | L | |
|---|---|---|
| H | \(\underline{\gamma_{HH}}, \underline{\gamma_{HH}}\) | \(\underline{1}, \underline{\gamma_{LH}}\) |
| L | \(\underline{\gamma_{LH}}, \underline{1}\) | \(\gamma_{LL}, \gamma_{LL}\) |
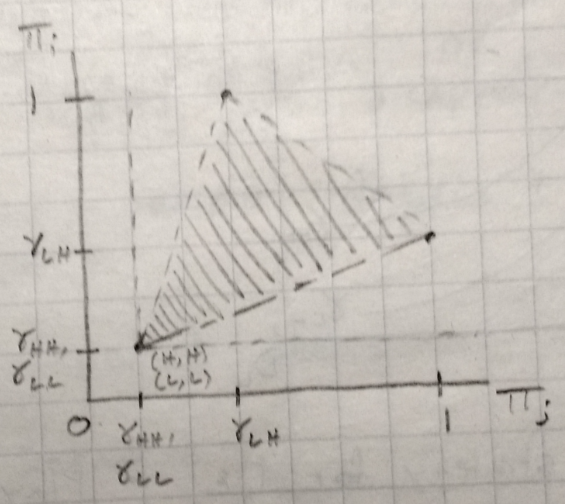
There are up to three Nash equilibria in pure strategies here: \((H,L), (L,H)\), and \((H,H)\). The \((H,H)\) equilibrium is possible if \(\gamma_{HH} = \gamma_{LH}\). I call this case “orbital separation”.
The folk region:
The intuition here is straightforward: pooling on the same orbit is worse than (or, if \(\gamma_{HH} = \gamma_{LH}\), as good as) mixing it up, so the firms mix it up.
Orbital separation has less overall risk and debris than orbital pooling. The firm which went low bears more risk than the firm which went high under orbital separation, but the orbits are cleaner overall. If we had more realistic debris dynamics (where debris could interact with other debris to generate more debris), orbital separation would be even better than orbital pooling.
There are four inferences we can draw about the process dynamics from this:
- If \(D_L\) is initially low but grows faster than \(Y_i\), orbital separation will transition to orbital pooling
- If \(D_L\) increases at the same rate as or a rate slower than \(Y_i\), orbital separation is sustainable
- If \(D_L\) decreases faster than \(Y_i\), orbital pooling can transition to orbital separation
- Orbital pooling will increase \(D_L\)
Let’s look at the debris dynamics a little more formally.
Putting some debris dynamics in
We’ll keep it simple here: debris in the low orbit will decay each period at a rate of \(\delta_D < 1\), and launches to the high orbit will generate \(\gamma\) many debris in the low orbit. Letting \(D_L'\) be the next period debris stock, the three cases for the debris law of motion are
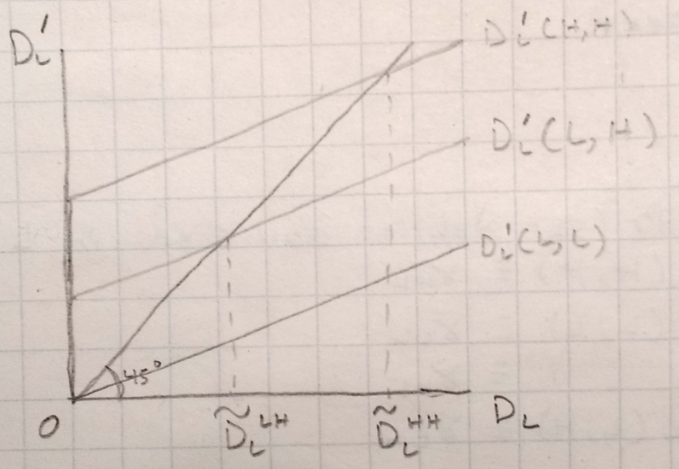
\[\begin{align} D_L'(L,L) ~&= (1 - \delta_D) D_L \cr D_L'(L,H) ~&= (1 - \delta_D) D_L + \gamma \cr D_L'(H,H) ~&= (1 - \delta_D) D_L + 2 \gamma \end{align}\]The diagram below shows the three possible fixed points of debris:
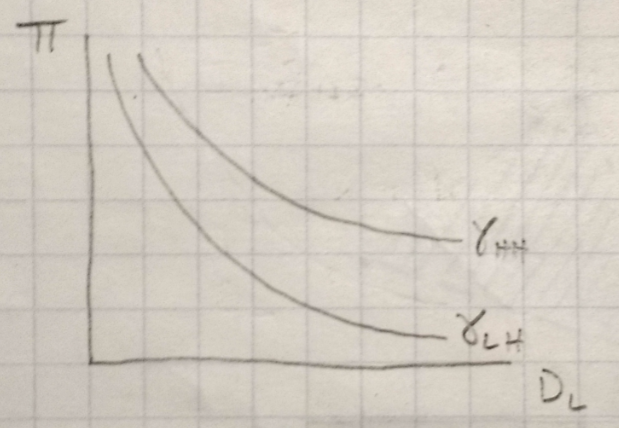
If both firms go low, the fixed point will be \(0\) debris in the low orbit. If the firms separate, it will be \(\tilde{D}_L^{LH}\). If the firms pool, it will be \(\tilde{D}_L^{HH}\). The next diagram shows the returns from orbital pooling and orbital separation as a function of the current period debris stock \(D_L\).
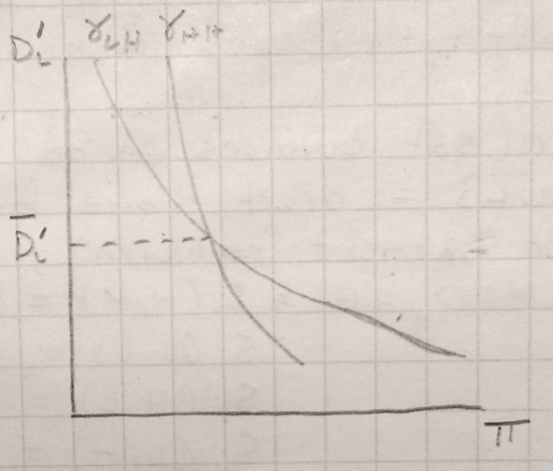
(The x and y axes are flipped because economics.) \(\bar{D}_L\) is a debris threshold. Above \(\bar{D}_L\), orbital pooling dominates orbital separation, and vice versa below \(\bar{D}_L\).
One question is whether the steady state debris level under orbital separation is higher or lower than the pooling-separation threshold, i.e. is \(\tilde{D}_L^{LH} \leq \bar{D}_L\).
If \(\tilde{D}_L^{LH} > \bar{D}_L\), then \(\tilde{D}_L^{LH}\) will occur, then firms will shift from orbital separation to orbital pooling, and \(\tilde{D}_L^{HH}\) will be the final debris steady state.
If \(\tilde{D}_L^{LH} \leq \bar{D}_L\), \(\tilde{D}_L^{LH}\) will occur, and firms will stay in orbital separation.
Below are payoff-debris plots for orbital separation and orbital pooling (with proper x-y axes):
Cooperation with a grim trigger
The folk region diagrams show us that cooperating to get higher payoffs is generally possible. One way to see what the cooperation could look like is to write a trigger strategy for an infinitely repeated game and then see when it will/won’t lead to cooperation.
The trigger strategy for firm \(i\) is:
- Play \(H,L,...\) if \(j\) plays \(L,H,...\)
- If firm \(j\) deviates, play \(H\) forever
Firm \(j\)’s strategy is defined similarly.
We can see that there’s no incentive to deviate from \((H,L)\) to \((L,L)\), only from \((L,H)\) to \((H,H)\). Assuming the firms share a discount factor \(\beta \in (0,1)\) and expanding out the series of payoffs, they’ll cooperate as long as
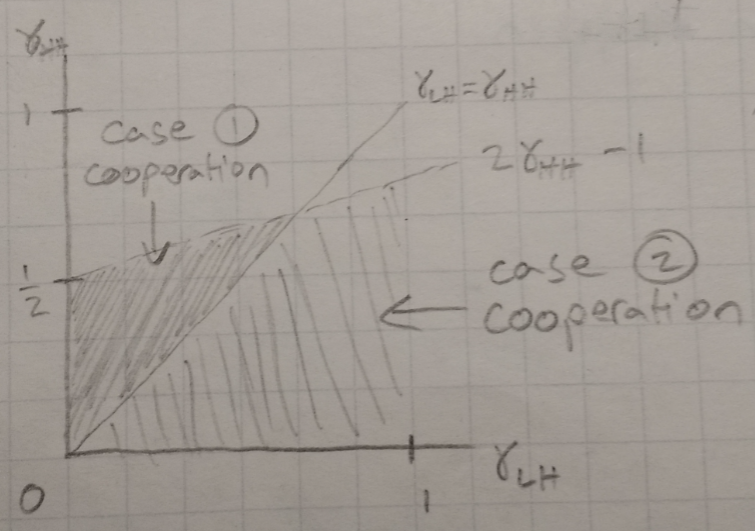
\[\begin{align} \gamma_{LH} + \beta + \beta^2 \gamma_{LH} + \beta^3 + ... & > \gamma_{HH} + \beta \gamma_{HH} + \beta^2 \gamma_{HH} + \beta^3 \gamma_{HH} + ... \cr \frac{\gamma_{LH} + 1}{2 (1 - \beta)} & > \frac{\gamma_{HH}}{1 - \beta} \cr \implies \gamma_{LH} & > 2 \gamma_{HH} - 1 \end{align}\]So, they can cooperate and alternate orbital separation with a grim trigger if \(\gamma_{LH} > 2 \gamma_{HH} - 1\). We can get a sense for how likely this cooperation is in a \(\gamma_{HH} - \gamma_{LH}\) payoff space,
So, cooperation seems more likely when orbital separation is already the Nash equilibrium. This seems intuitive enough to me.
Concluding thoughts
This is obviously a very stylized model, but I think the general notion of orbital separation vs orbital pooling is more generally applicable. I think this conclusion is kinda neat.
With more altitudes, I would expect the pooling/separation dynamic to result in firms moving progressively higher in LEO. I think we can sort of see that in SpaceX and OneWeb’s altitude choices for their announced constellations - around 1,200 and 1,100 km up, close to or a little higher than the LEO altitudes which are most-used right now. Obviously there’s a lot more than collision risk going into the choice of altitude for a constellation, but I expect the risk to be a factor.
Adding the benefits to a particular altitude (e.g. coverage area) parameterizes the problem some more, but doesn’t seem to add any interesting economic dynamics. Launch costs are necessary in the dynamic decision model, but can be ignored here. Allowing satellites to last more than one period really complicates the economic dynamics, as does adding more firms or altitudes. The physical dynamics are cool and have been studied fairly well, but the economic dynamics have not really been studied at all. I may be biased - I think the exciting action in the space debris problem is in the economic dynamics.
I would really like to model constellation size choices, but again the economic dynamics make it really complicated. I wrote a single-shell model of comparative steady state constellation choices with free entry and debris accumulation for a class last semester which I might be able to extend with altitudes. The steady states are not easy to compute - mechanically, the problem is that the debris accumulation can make the cost function concave, making the firm’s optimization problem nonconvex. Getting the full transition paths would be cool and presumably even harder. I’m working on this, but I don’t expect to get the most general case with constellations, multiple firms, multiple altitudes, and debris accumulation any time soon.